CZSL 超像素增强复现与优化实战：从视觉纠缠到多尺度融合

项目仓库：https://github.com/GongyiChuren/czsl-Superpixel

1. 问题背景：为什么 CZSL 在视觉上容易“纠缠”#

组合零样本学习（Compositional Zero-Shot Learning, CZSL）的目标是：

训练阶段只见过部分属性-物体组合；
测试阶段要识别未见过的新组合（如训练见过 red apple 和 blue car，测试要识别 red car）。

这要求模型学到“可组合”的表示，即属性和物体要能在特征空间中相对解耦。

实际困难在于，常规 CNN 往往偏向纹理统计，面对噪声/复杂背景时容易把无关纹理当作判别依据，导致：

结构信息（轮廓、局部几何）被淹没；
属性和物体表征互相污染；
未见组合泛化能力下降。

我在这个项目中的思路是：先复现超像素增强（SVFE）作为结构先验，再优化成多尺度融合，改善“去噪 vs 细节保留”的矛盾。

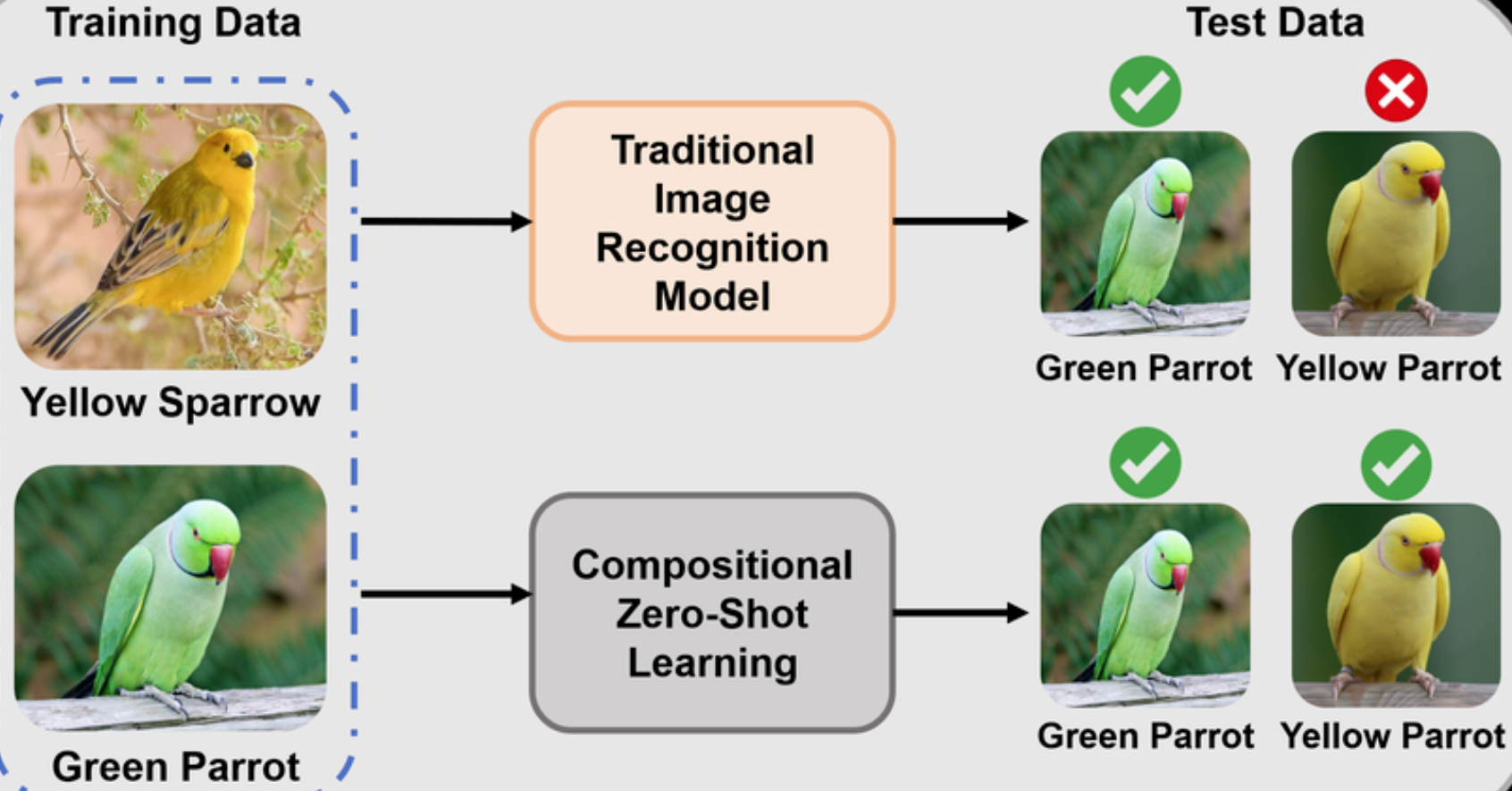
Figure 1. 视觉纠缠问题定义：纹理干扰会破坏属性-物体解耦。

2. 复现部分：Superpixel-based Visual Feature Enhancement#

复现核心代码在：czsl-Superpixel-code/czsl-Superpixel-based/superpixel_module.py

2.1 从像素到超像素区域#

给定图像特征图（这里先以图像 RGB 演示，后续可替换为中间层特征）

X \in \mathbb{R}^{C\times H\times W}

用 SLIC 得到超像素分区：

\{S_i\}_{i=1}^{M},\quad S_i \subseteq \{1,\dots,H\}\times\{1,\dots,W\}

其中 $M$ 是超像素数量， $S_i$ 表示第 $i$ 个区域的像素集合。

2.1.1 SLIC 本身的推导#

SLIC（Simple Linear Iterative Clustering）可以看成在 5 维空间做局部约束的 k-means [3]。对每个像素 $p$ ，定义：

\mathbf{v}_p = [l_p, a_p, b_p, x_p, y_p]^\top

其中 $(l,a,b)$ 是 Lab 颜色空间， $(x,y)$ 是像素坐标。

对于第 $k$ 个超像素中心：

\mathbf{c}_k = [l_k, a_k, b_k, x_k, y_k]^\top

定义颜色距离和空间距离：

d_c = \sqrt{(l_p-l_k)^2 + (a_p-a_k)^2 + (b_p-b_k)^2},\quad d_s = \sqrt{(x_p-x_k)^2 + (y_p-y_k)^2}

SLIC 的归一化距离：

D(p,k)=\sqrt{\left(\frac{d_c}{m}\right)^2 + \left(\frac{d_s}{S}\right)^2}

其中：

$S \approx \sqrt{\frac{N}{K}}$ 是网格步长（ $N$ 为像素总数， $K$ 为超像素数）；
$m$ 是紧致度参数（compactness），控制“颜色一致性”和“空间紧致性”的权衡。

在这个定义下，SLIC 迭代等价于最小化如下目标：

\min_{\{S_k,\mathbf{c}_k\}} \sum_{k=1}^{K}\sum_{p\in S_k} D(p,k)^2

优化过程与 k-means 一致，分两步交替：

分配步（Assignment）：对像素分配最近中心

\text{label}(p)=\arg\min_k D(p,k)

更新步（Update）：按当前簇均值更新中心

\mathbf{c}_k \leftarrow \frac{1}{|S_k|}\sum_{p\in S_k}\mathbf{v}_p

由于每个中心只在局部窗口（约 $2S\times2S$ ）内搜索，而不是全局搜索，SLIC 复杂度接近线性，且分块边界通常贴合图像结构，这也是它适合做超像素先验的原因。

2.1.2 参数到底在控制什么（结合我的实验）#

PPT 里我反复强调两个参数：n_segments 和 compactness。这两个参数不是“随便调”，它们直接决定模型看到的信息形态。

n_segments（分块数）
- 小：每块更大，更像“强平滑”，抗噪好，但容易吃掉细节；
- 大：每块更小，细节保留更好，但也更容易把噪声留住。
compactness（紧致度，对应上面的 $m$ $m$ ）
- 小：更偏颜色一致性，边界更贴物体真实轮廓；
- 大：更偏空间规整，块会更“圆/方”，但可能跨越真实边界。

我在 demo 和实验中看到的现象是：

n_segments=100 时分块很粗，适合看整体结构；
n_segments=1000 时边界明显更贴局部轮廓；
继续增大分块数时，细节会更完整，但抗噪能力会下降。

这正是后面做多尺度融合的动机：单一尺度很难同时满足“结构稳定”和“细节保真”。

Figure 2. 超像素 Demo：分割粒度会直接影响抗噪和轮廓保持。

2.2 区域聚合公式推导#

区域级表示定义为区域内均值池化：

\hat{f}_i = \frac{1}{|S_i|}\sum_{p\in S_i} f_p,\quad \hat{f}_i\in\mathbb{R}^{C}

把所有区域拼接得到：

\hat{F} = [\hat{f}_1,\hat{f}_2,\dots,\hat{f}_M] \in \mathbb{R}^{C\times M}

它可以理解为一种结构约束下的降噪：区域内高频噪声在均值时被抵消，而同一区域的稳定语义被保留。

2.3 为什么这种聚合有效#

假设像素特征可以写成：

f_p = s_p + \epsilon_p

其中 $s_p$ 是有用语义信号， $\epsilon_p$ 是零均值噪声，且同一区域内噪声近似独立。则：

\hat{f}_i = \frac{1}{|S_i|}\sum_{p\in S_i}s_p + \frac{1}{|S_i|}\sum_{p\in S_i}\epsilon_p

第二项方差大致按 $1/|S_i|$ 缩小，所以聚合后表示更稳定。这就是超像素增强能提升鲁棒性的统计基础。

3. 优化部分：多尺度融合（V2）#

优化代码在：czsl-Superpixel-code/czsl-Superpixel-based/V2.py

单尺度复现方法有一个典型 trade-off：

区域太大：去噪强，但细节被抹平；
区域太小：细节保留好，但抗噪弱。

3.1 双路特征构建#

我采用两个尺度并行（与 PPT 中的 V2 一致）：

粗尺度（结构层）：n_segments=1500，强调轮廓稳定与去噪；
细尺度（纹理层）：n_segments=6000，保留边缘和纹理细节。

记两路输出为：

F_c,\;F_f

融合输出：

F_{\text{fuse}} = \alpha F_c + (1-\alpha)F_f

当前实验使用固定权重（实现里是 0.5/0.5），后续可以把 $\alpha$ 改成可学习参数或门控函数。

这里的直觉可以写得更“工程化”一点：

粗尺度输出像一个稳定的低频底座；
细尺度输出像高频补偿；
融合就是“先稳住，再补细节”。

3.2 为什么多尺度更合理#

从偏差-方差视角看：

粗尺度降低方差（抗噪）；
细尺度降低偏差（保细节）；
线性融合可在两者之间找平衡。

因此在复杂场景下，V2 往往比 V1 更稳。

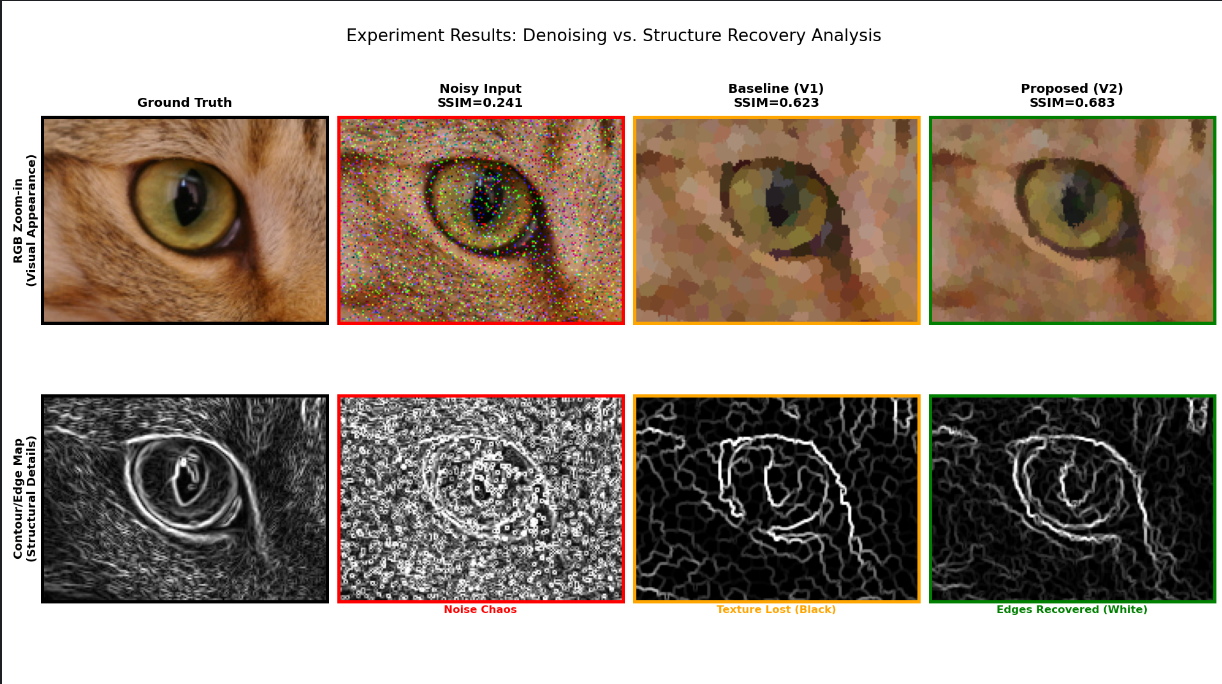
Figure 3. V2 多尺度融合：粗尺度去噪，细尺度保边缘，SSIM 提升。

4. 实验设计与指标#

4.0 先踩的坑：ResNet 分类分数并不能直接证明改进#

我一开始用 ResNet50 分类误差来验证“图像是否更好识别”，结果出现了反直觉现象：

Baseline（噪声图）误差约 29.1
Ours（超像素修复图）误差约 75.5

这并不代表方法失败，而是揭示了 ResNet 的纹理偏置 [2]：

超像素处理本质上会压低高频纹理；
ResNet 在很多场景恰恰高度依赖纹理；
所以“结构更好”不等于“ResNet 分类分更高”。

因此我在 PPT 里把评估切换到结构指标 SSIM，并辅以边缘响应和 t-SNE 可视化，这样更符合 CZSL 关注的“结构可组合性”。

探索 I：ResNet 误差反直觉	探索 II：SSIM 成功验证
ResNet误差反直觉	SSIM成功验证

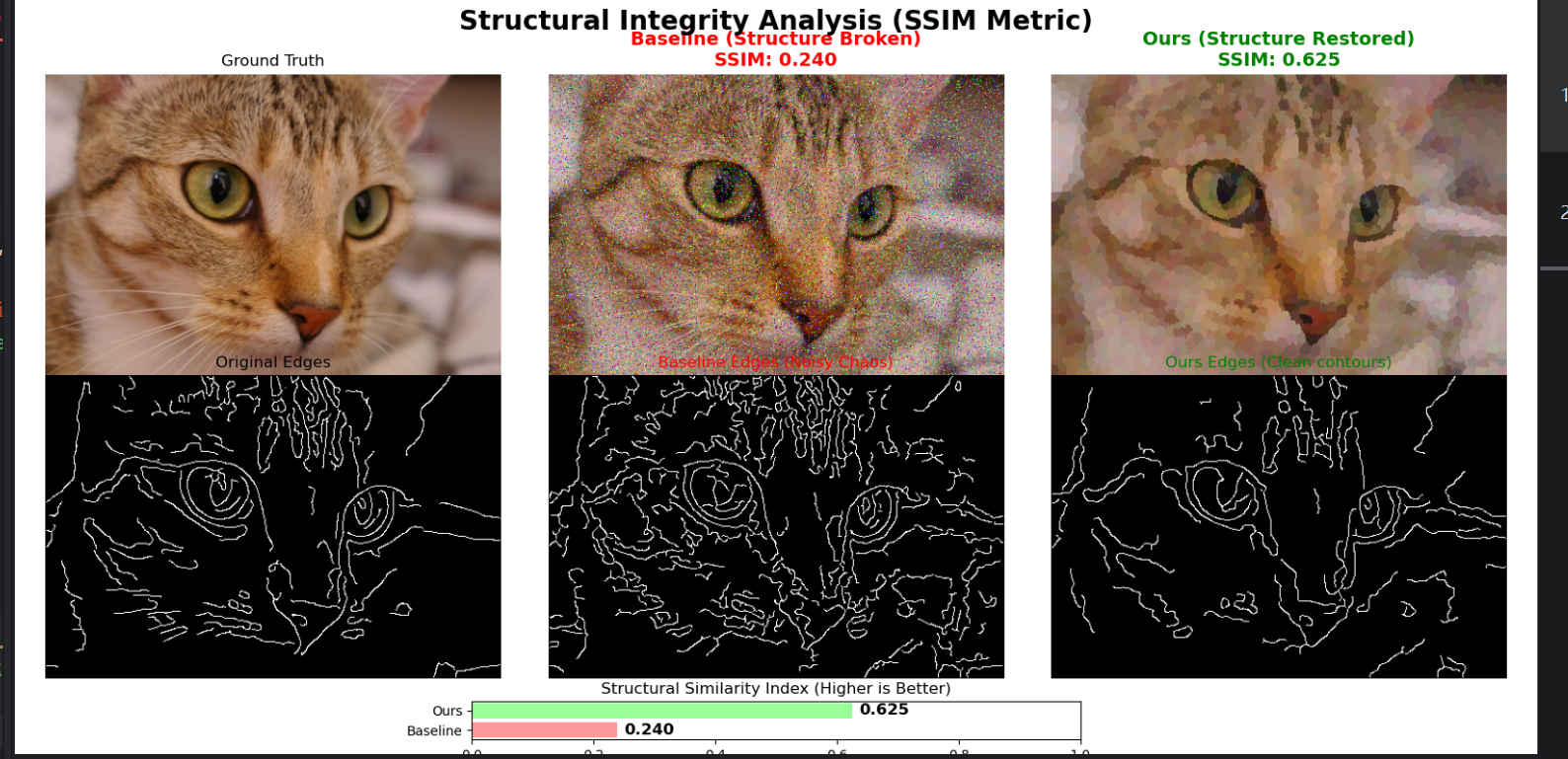Figure 4. 评估路径切换：分类分数不稳定，结构指标更贴合目标。

4.1 噪声鲁棒性实验#

脚本：czsl-Superpixel-code/czsl-Superpixel-based/Noise_Robustness.py

流程：

构造高强度椒盐噪声输入；
分别用 Baseline（V1）和 Ours（V2）处理；
计算与干净图的结构相似性 SSIM；
辅助可视化边缘图（结构恢复证据）。

SSIM 定义：

\mathrm{SSIM}(x,y)=\frac{(2\mu_x\mu_y + c_1)(2\sigma_{xy}+c_2)}{(\mu_x^2+\mu_y^2+c_1)(\sigma_x^2+\sigma_y^2+c_2)}

其中 $\mu$ 为均值， $\sigma^2$ 为方差， $\sigma_{xy}$ 为协方差。SSIM 越高，结构保真度越好。

4.2 判别性实验（相似类别 + 强干扰）#

脚本：czsl-Superpixel-code/czsl-Superpixel-based/t_SNE_Experiment.py

设置要点：

选择容易混淆的相似类别（Cat/Deer/Dog）；
施加强噪声扰动；
比较 Baseline 与 Ours 的特征分布；
用 t-SNE 观察类间可分性与类内紧致性。

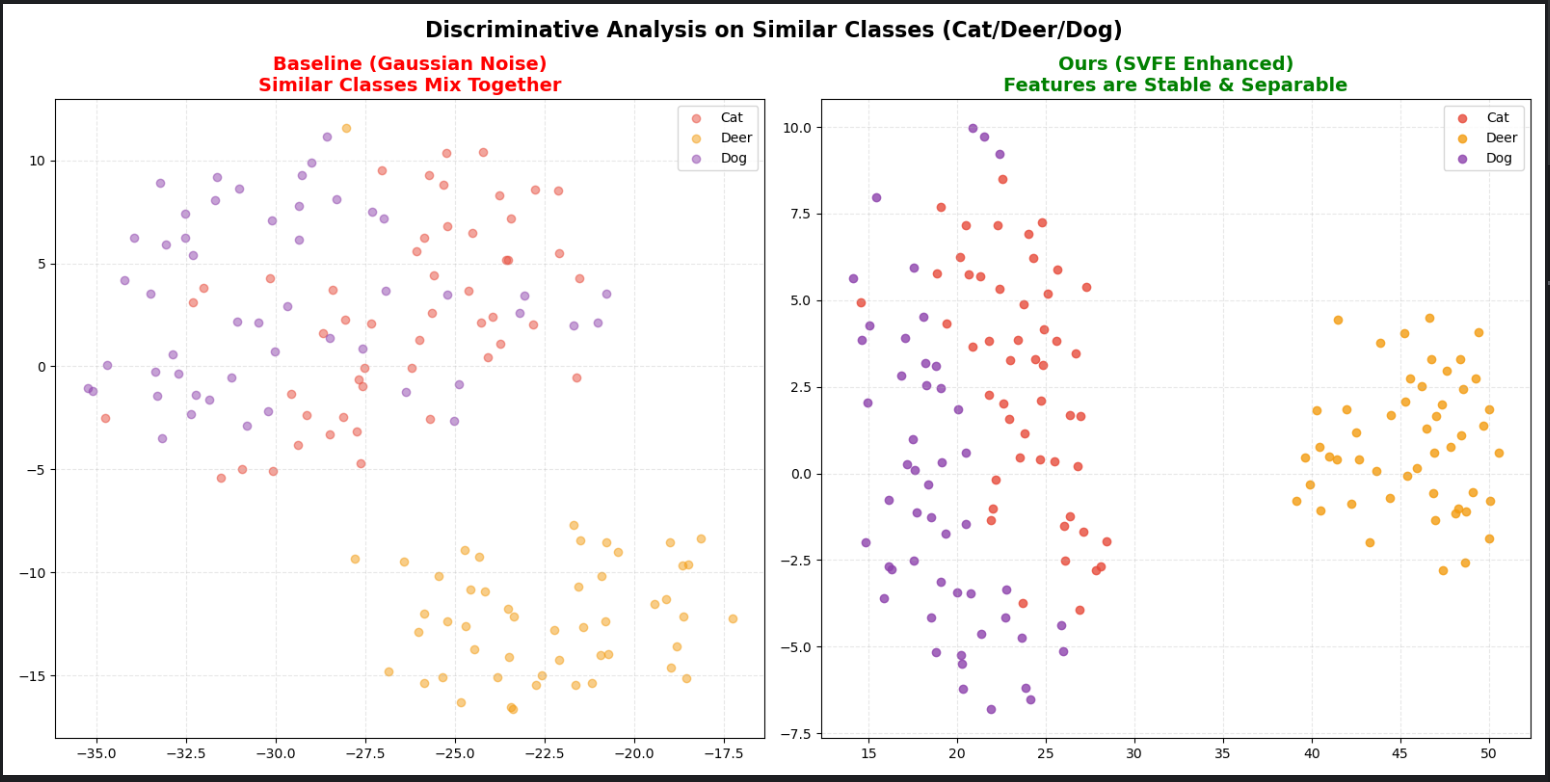
Figure 5. t-SNE 可分性验证：强噪声下 Ours 仍保持更清晰簇分离。

4.3 实验环境与数据集#

数据集 1：MIT-States，约 53,753 张图像，115 个属性，背景复杂，适合验证前景/背景分离能力；
数据集 2：UT-Zappos（文中也写作 Zappos），约 50,025 张图像，鞋类细粒度差异明显，适合验证细微材质识别。

工程配置方面，本地实验环境使用 RTX Laptop GPU（8GB 显存）进行复现与验证；训练流程由 flags.py、train.py、test.py 管理。

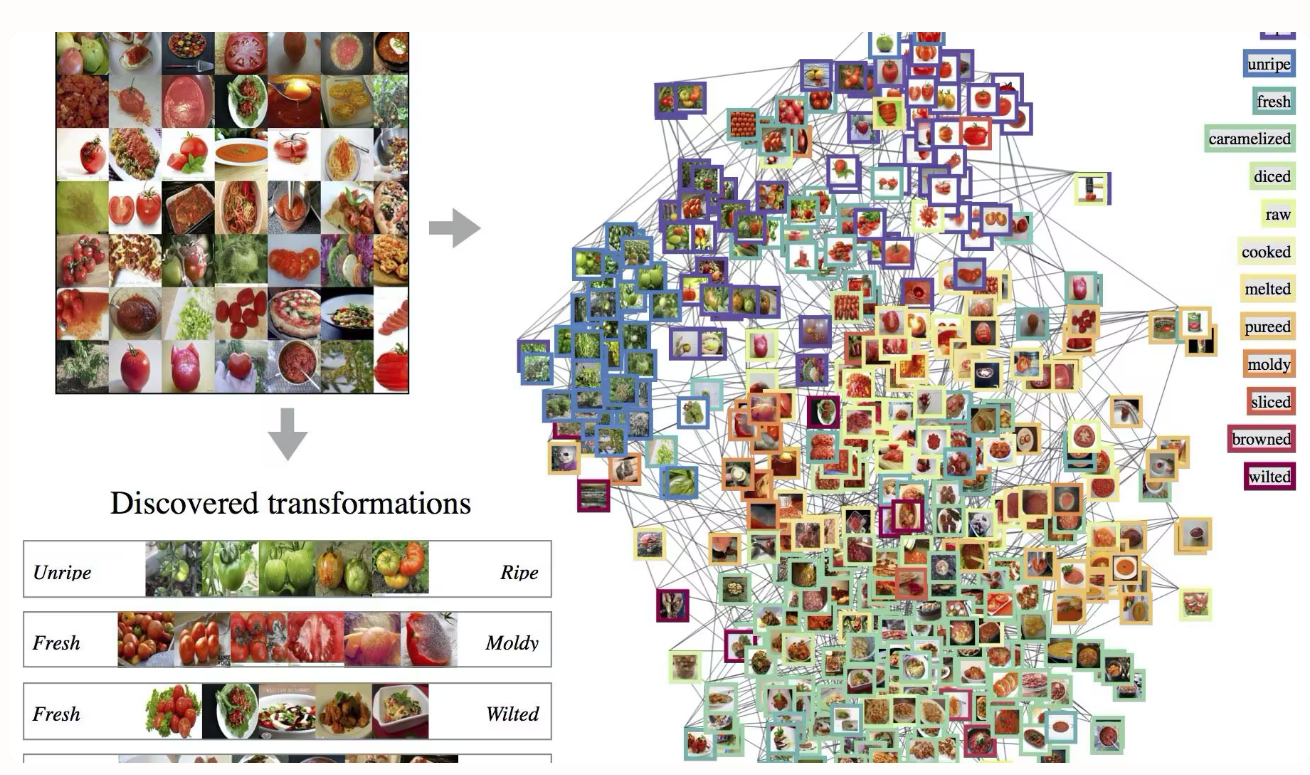
Figure 6. 数据集与任务挑战概览。

5. 关键结论#

复现有效：超像素区域聚合确实能缓解噪声导致的结构破坏。
优化有效：多尺度融合在 SSIM 和可视化上都优于单尺度基线（0.625 -> 0.683）。
机制合理：粗细双路分别承担抗噪和保细节角色，符合统计与表示学习直觉。

6. 还能怎么继续做#

下一步我准备沿这几条线继续推进：

把融合权重从常数升级为可学习门控；
将多尺度模块更深地接入完整 CZSL 训练管线，做标准 benchmark 对比；
增加更多噪声类型和跨数据域验证，评估泛化稳定性。

7. 相关文件索引#

详细文字说明：report.docx
汇报版图文：ppt_report.pptx
复现核心：czsl-Superpixel-code/czsl-Superpixel-based/superpixel_module.py
优化实验：czsl-Superpixel-code/czsl-Superpixel-based/V2.py
鲁棒性验证：czsl-Superpixel-code/czsl-Superpixel-based/Noise_Robustness.py
判别性可视化：czsl-Superpixel-code/czsl-Superpixel-based/t_SNE_Experiment.py

如果你也在做“复现 + 改进”类课程项目，欢迎直接参考这个结构：先做可运行复现，再做单点优化，再用定量指标和可视化双重验证，最后写成可复查的技术闭环。

8. 参考文献#

[1] Du, W., Bao, X., Xu, X., et al. (2026). Superpixel-based Visual Feature Enhancement for Compositional Zero-Shot Learning. Information Processing and Management.

[2] He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep Residual Learning for Image Recognition. CVPR.

[3] Achanta, R., et al. (2012). SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE TPAMI.

GongyiChuren